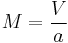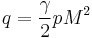Mach number
Mach number ( or
or  ) (generally /ˈmɑːk/, sometimes /ˈmɑːx/ or /ˈmæk/) is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure. It is commonly used to represent the speed of an object when it is traveling close to or above the speed of sound.
) (generally /ˈmɑːk/, sometimes /ˈmɑːx/ or /ˈmæk/) is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure. It is commonly used to represent the speed of an object when it is traveling close to or above the speed of sound.
where
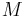 is the Mach number
is the Mach number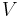 is the relative velocity of the source to the medium and
is the relative velocity of the source to the medium and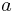 is the speed of sound in the medium
is the speed of sound in the medium
The Mach number is named after Austrian physicist and philosopher Ernst Mach, a designation proposed by aeronautical engineer Jakob Ackeret. Because the Mach number is often viewed as a dimensionless quantity rather than a unit of measure, with Mach, the number comes after the unit; the second Mach number is "Mach 2" instead of "2 Mach" (or Machs). This is somewhat reminiscent of the early modern ocean sounding unit "mark" (a synonym for fathom), which was also unit-first, and may have influenced the use of the term Mach. In the decade preceding faster-than-sound human flight, aeronautical engineers referred to the speed of sound as Mach's number, never "Mach 1."[1]
In French, the Mach number is sometimes called the "nombre de Sarrau" ("Sarrau number") after Émile Sarrau, researching on explosions in the 1870s and 1880s.[2]
Contents |
Overview
The Mach number is commonly used both with objects traveling at high speed in a fluid, and with high-speed fluid flows inside channels such as nozzles, diffusers or wind tunnels. As it is defined as a ratio of two speeds, it is a dimensionless number. At Standard Sea Level conditions (corresponding to a temperature of 15 degrees Celsius), the speed of sound is 340.3 m/s[3] (1225 km/h, or 761.2 mph, or 661.5 knots, or 1116 ft/s) in the Earth's atmosphere. The speed represented by Mach 1 is not a constant; for example, it is mostly dependent on temperature and atmospheric composition and largely independent of pressure. Since the speed of sound increases as the temperature increases, the actual speed of an object traveling at Mach 1 will depend on the fluid temperature around it. Mach number is useful because the fluid behaves in a similar way at the same Mach number. So, an aircraft traveling at Mach 1 at 20°C or 68°F, at sea level, will experience shock waves in much the same manner as when it is traveling at Mach 1 at 11,000 m (36,000 ft) at -50°C or -58F, even though it is traveling at only 86% of its speed at higher temperature like 20°C or 68°F.
High-speed flow around objects
Flight can be roughly classified in six categories:
| Regime | Subsonic | Transonic | Sonic | Supersonic | Hypersonic | High-hypersonic |
|---|---|---|---|---|---|---|
| Mach | <1.0 | 0.8–1.2 | 1.0 | 1.2–5.0 | 5.0–10.0 | >10.0 |
For comparison: the required speed for low Earth orbit is approximately 7.5 km/s = Mach 25.4 in air at high altitudes. The speed of light in a vacuum corresponds to a Mach number of approximately 881,000 (relative to air at sea level).
At transonic speeds, the flow field around the object includes both sub- and supersonic parts. The transonic period begins when first zones of M>1 flow appear around the object. In case of an airfoil (such as an aircraft's wing), this typically happens above the wing. Supersonic flow can decelerate back to subsonic only in a normal shock; this typically happens before the trailing edge. (Fig.1a)
As the speed increases, the zone of M>1 flow increases towards both leading and trailing edges. As M=1 is reached and passed, the normal shock reaches the trailing edge and becomes a weak oblique shock: the flow decelerates over the shock, but remains supersonic. A normal shock is created ahead of the object, and the only subsonic zone in the flow field is a small area around the object's leading edge. (Fig.1b)
| (a) | (b) |
Fig. 1. Mach number in transonic airflow around an airfoil; M<1 (a) and M>1 (b).
When an aircraft exceeds Mach 1 (i.e. the sound barrier) a large pressure difference is created just in front of the aircraft. This abrupt pressure difference, called a shock wave, spreads backward and outward from the aircraft in a cone shape (a so-called Mach cone). It is this shock wave that causes the sonic boom heard as a fast moving aircraft travels overhead. A person inside the aircraft will not hear this. The higher the speed, the more narrow the cone; at just over M=1 it is hardly a cone at all, but closer to a slightly concave plane.
At fully supersonic speed, the shock wave starts to take its cone shape and flow is either completely supersonic, or (in case of a blunt object), only a very small subsonic flow area remains between the object's nose and the shock wave it creates ahead of itself. (In the case of a sharp object, there is no air between the nose and the shock wave: the shock wave starts from the nose.)
As the Mach number increases, so does the strength of the shock wave and the Mach cone becomes increasingly narrow. As the fluid flow crosses the shock wave, its speed is reduced and temperature, pressure, and density increase. The stronger the shock, the greater the changes. At high enough Mach numbers the temperature increases so much over the shock that ionization and dissociation of gas molecules behind the shock wave begin. Such flows are called hypersonic.
It is clear that any object traveling at hypersonic speeds will likewise be exposed to the same extreme temperatures as the gas behind the nose shock wave, and hence choice of heat-resistant materials becomes important.
High-speed flow in a channel
As a flow in a channel becomes supersonic, one significant change takes place. The conservation of mass flow rate leads one to expect that contracting the flow channel would increase the flow speed (i.e. making the channel narrower results in faster air flow) and at subsonic speeds this holds true. However, once the flow becomes supersonic, the relationship of flow area and speed is reversed: expanding the channel actually increases the speed.
The obvious result is that in order to accelerate a flow to supersonic, one needs a convergent-divergent nozzle, where the converging section accelerates the flow to sonic speeds, and the diverging section continues the acceleration. Such nozzles are called de Laval nozzles and in extreme cases they are able to reach hypersonic speeds (Mach 13 at 20°C).
An aircraft Machmeter or electronic flight information system (EFIS) can display Mach number derived from stagnation pressure (pitot tube) and static pressure.
Calculation
Assuming air to be an ideal gas, the formula to compute Mach number in a subsonic compressible flow is derived from Bernoulli's equation for M<1:[4]
where:
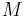 is Mach number
is Mach number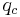 is impact pressure and
is impact pressure and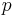 is static pressure
is static pressure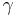 is the ratio of specific heat of a gas at a constant pressure to heat at a constant volume (1.4 for air).
is the ratio of specific heat of a gas at a constant pressure to heat at a constant volume (1.4 for air).
The formula to compute Mach number in a supersonic compressible flow is derived from the Rayleigh Supersonic Pitot equation:
or for air, a simplfied formula:
where:
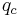 is now impact pressure measured behind a normal shock.
is now impact pressure measured behind a normal shock.
The Mach number at which an aircraft is flying at can be calculated by
where:
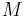 is Mach number
is Mach number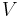 is velocity of the moving aircraft and
is velocity of the moving aircraft and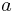 is the speed of sound at the given altitude
is the speed of sound at the given altitude
Note that the dynamic pressure can be found as:
See also
Notes
- ^ Bodie, Warren M., The Lockheed P-38 Lightning, Widewing Publications ISBN 0-9629359-0-5
- ^ Blackmore, John T. (1972). Ernst Mach: His Life, Work, and Influence. University of California Press. p. 112. ISBN 9780520018495.
- ^ Clancy, L.J. (1975), Aerodynamics, Table 1, Pitman Publishing London, ISBN 0 273 01120 0
- ^ Olson, Wayne M. (2002). "AFFTC-TIH-99-02, Aircraft Performance Flight Testing." (PDF). Air Force Flight Test Center, Edwards AFB, CA, United States Air Force.
External links
- Gas Dynamics Toolbox Calculate Mach number and normal shock wave parameters for mixtures of perfect and imperfect gases.
- NASA's page on Mach Number Interactive calculator for Mach number.
- NewByte standard atmosphere calculator and speed converter
|
|||||
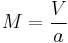
![{M}=\sqrt{\frac{2}{\gamma-1}\left[\left(\frac{q_c}{p}%2B1\right)^\frac{\gamma-1}{\gamma}-1\right]}\,](/2012-wikipedia_en_all_nopic_01_2012/I/f5f17abcc7ba9752a2c5c2bbbec0be13.png)
![\frac{q_c}{p} = \left[\left(\frac{\gamma%2B1}{2}\right)M^2\right]^\left(\frac{\gamma}{\gamma-1}\right)\cdot \left[ \frac{\gamma%2B1}{\left(1-\gamma%2B2 \gamma \cdot M^2\right)^\left(\frac{1}{ \gamma-1 }\right)} \right]^\left(\frac{1}{ \gamma-1 }\right)-1](/2012-wikipedia_en_all_nopic_01_2012/I/a87cdc9345b6c152b969185e1840c49d.png)
![{M}=0.88128485\sqrt{\left[\left(\frac{q_c}{p}%2B1\right)\left(1-\frac{1}{[7M^2]}\right)^{2.5}\right]}](/2012-wikipedia_en_all_nopic_01_2012/I/5f42bdc0482a7550a5bde798163761aa.png)